Java Ring Buffer
Jakob Jenkov |
A ring buffer is an array which is used as a queue. The ring buffer has a read position and a write position which marks the next position to read from and write to the ring buffer. When the write position reaches the end of the array, the write position is set back to 0. The same is true for the read position.
Setting the read and write position back to zero when they reach then end of the array is also sometimes referred to as "wrapping around". It is this behaviour which turns the array into a ring buffer. When the read and write position reaches the end of the array they continue from the beginning of the array, just as if the array was a ring. Hence the name ring buffer.
This ring buffer tutorial will explain how a ring buffer works and show two Java ring buffer implementations.
How a Ring Buffer Works
A ring buffer is an array with a fixed size, just like a bounded queue. The array contains the elements stored in the ring buffer.
In addition to the array containing the elements, a ring buffer contains a write position which points to the position in the array where the next element is to be inserted into.
A ring buffer also needs to keep track of the read position - the next position in the array to read an element from.
A ring buffer also needs to keep track of the free and used space in the element array. When the write position has not wrapped around, the used space is between the write position and the read position. All the rest is free space. The diagram below illustrates a ring buffer in this situation:
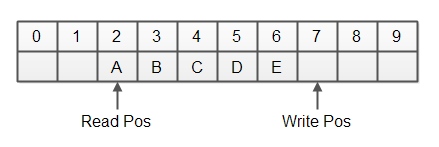
When the write position has wrapped around the situation is different. All of a sudden the free space is the space between the write position and the read position. All the rest is used space. Here is a diagram illustrating the same ring buffer after the write position has wrapped around:
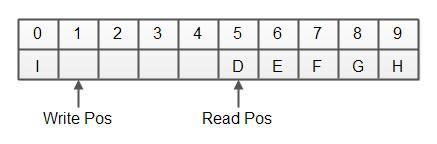
There are different ways to keep track of the read position (and thus used and free space) in a ring buffer. Later in this tutorial I will explain two different ways to implement a ring buffer in Java.
Ring Buffers Are Fast
Ring buffers are a fast way to implement queue-like structures. By "fast" I mean both that they are reasonably easy to implement, and that they perform quite well.
Ring Buffer Use Cases
Ring buffers are useful both for actual queues, like a queue of messages, or for producing data which is later consumed in a streaming-like fashion.
Ring buffers are especially useful when you need a hard upper bound for how much data can be in the ring buffer (in the queue).
If you don't want an upper bound on your queue structure, perhaps you should be using a linked list, or a ring buffer that can resize itself (allocate a new, bigger array when it is full, and move all elements to that array).
In this tutorial I will only focus on the bounded ring buffer implementations.
Ring Buffer Implementation Techniques
There are many ways to implement ring buffers. In this ring buffer tutorial I will show you two of the easiest techniques to implement a ring buffer. These techniques are:
- Using a fill count
- Using a flip marker
I will explain both techniques in the following sections.
Ring Buffer Using Fill Count
One way to keep track of write position, read position and the number of elements in the ring buffer is to use a write position and a fill count. The write position marks the next position in the ring buffer to write an element to. The fill count tells how many elements are currently stored in the buffer.
When writing elements to the ring buffer it just has to check the fill count to see if it is full or not. If it is not full the element can be inserted at the write position and the write position advanced to the next free slot.
Similarly, when reading elements from the ring buffer it just has to check the fill count to see if the ring buffer is empty. The read position is calculated by subtracting the fill count from the write position. If the result of that calculation is negative, the write position has wrapped around, and you need to add the size of the buffer (array) to the read position to get the correct read position.
Below is a ring buffer implementation that uses a fill count. Notice that it does not track the read position
explicitly, but calculates the read position based on the write position and the fill count. Notice also,
that the fill count field is called available (not fillCount).
public class RingBufferFillCount {
public Object[] elements = null;
private int capacity = 0;
private int writePos = 0;
private int available = 0;
public RingBufferFillCount(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
}
public void reset() {
this.writePos = 0;
this.available = 0;
}
public int capacity() { return this.capacity; }
public int available(){ return this.available; }
public int remainingCapacity() {
return this.capacity - this.available;
}
public boolean put(Object element){
if(available < capacity){
if(writePos >= capacity){
writePos = 0;
}
elements[writePos] = element;
writePos++;
available++;
return true;
}
return false;
}
public Object take() {
if(available == 0){
return null;
}
int nextSlot = writePos - available;
if(nextSlot < 0){
nextSlot += capacity;
}
Object nextObj = elements[nextSlot];
available--;
return nextObj;
}
}
Ring Buffer Using Flip Marker
Another option to keep track of read position, write position and how many elements are in the buffer, is to simply keep a read position in addition to the write position.
How many elements are in the buffer is calculated based on the write and read position. How the calculation looks depends on whether the write position has flipped (wrapped around) or not.
If the write position has not wrapped around you can simply subtract the read position from the write position to know how many elements are in the buffer. If the write position has wrapped around (flipped) then the available space is equal to the capacity minus the read position plus the write position.
To keep track of whether the write position has flipped or not a special "flip marker" is used. That is where the name of the implementation comes from. Actually, in most cases you could just check if the write position is larger or smaller than the read position to detect if the write position has wrapped around. But, that doesn't work when write position and read position are equal (the ring buffer is either completely full or completely empty).
Below is an implementation of a ring buffer that uses a flip marker and read position.
public class RingBufferFlipMarker {
public Object[] elements = null;
public int capacity = 0;
public int writePos = 0;
public int readPos = 0;
public boolean flipped = false; //the flip marker
public RingBufferFlipMarker(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
}
public void reset() {
this.writePos = 0;
this.readPos = 0;
this.flipped = false;
}
public int available() {
if(!flipped){
return writePos - readPos;
}
return capacity - readPos + writePos;
}
public int remainingCapacity() {
if(!flipped){
return capacity - writePos;
}
return readPos - writePos;
}
public boolean put(Object element){
if(!flipped){
if(writePos == capacity){
writePos = 0;
flipped = true;
if(writePos < readPos){
elements[writePos++] = element;
return true;
} else {
return false;
}
} else {
elements[writePos++] = element;
return true;
}
} else {
if(writePos < readPos ){
elements[writePos++] = element;
return true;
} else {
return false;
}
}
}
public Object take() {
if(!flipped){
if(readPos < writePos){
return elements[readPos++];
} else {
return null;
}
} else {
if(readPos == capacity){
readPos = 0;
flipped = false;
if(readPos < writePos){
return elements[readPos++];
} else {
return null;
}
} else {
return elements[readPos++];
}
}
}
}
Ring Buffer Performance
My benchmarks have shown that the ring buffer using a fill count is a little bit faster than the ring buffer using a flip marker. But - the difference is so small that it is almost insignificant.
Batch Modes
I have implemented batch mode put() and take() operations for both ring buffer
implementations. The implementations with batch operations are listed later in this tutorial. Putting and getting
several elements at a time is significantly faster than putting and getting a single element at a time.
My benchmarks showed that batch put() and take() operations provides up to 4 times
the throughput of putting and taking a single element at a time. Precisely how much depends on the batch size. L
arger batches yields a higher throughput than smaller batches because more time is spent in tight array copy loops.
The batch operations of the ring buffer implementation using a read position + flip marker was around 15% faster than the batch operations of the ring buffer using a fill count.
Concurrency
Neither of the two implementations shown above are thread safe. They can only be used from the same thread.
It is my impression that the implementation using a read position and flip marker is easier to implement in thread safe version for the single reader, single writer case. The single reader, single writer case means that only one thread is putting elements to the ring buffer. And I mean only one thread ever. Not at the same time. Only that one same thread. The same principle goes for the writing thread. Only that one and same thread only ever writes to the ring buffer. The reading thread does not have to be the same as the writing thread though.
I have not yet implemented any single reader, single writer version of the ring buffer, so I don't actually know. I will update this tutorial if I one day do.
Ring Buffer Using Fill Count - Including Batch Operations
Here is an implementation of the ring buffer that uses a fill count including the batch put()
and take() operations.
public class RingBufferFillCount {
public Object[] elements = null;
public int capacity = 0;
public int writePos = 0;
public int available = 0;
public RingBufferFillCount(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
}
public void reset() {
this.writePos = 0;
this.available = 0;
}
public int remainingCapacity() {
return this.capacity - this.available;
}
public boolean put(Object element){
if(available < capacity){
if(writePos >= capacity){
writePos = 0;
}
elements[writePos] = element;
writePos++;
available++;
return true;
}
return false;
}
public int put(Object[] newElements){
return put(newElements, newElements.length);
}
public int put(Object[] newElements, int length){
int readPos = 0;
if(this.writePos > this.available){
//space above writePos is all empty
if(length <= this.capacity - this.writePos){
//space above writePos is sufficient to insert batch
for(; readPos < length; readPos++){
this.elements[this.writePos++] = newElements[readPos];
}
this.available += readPos;
return length;
} else {
//both space above writePos and below writePos is necessary to use
//to insert batch.
int lastEmptyPos = writePos - available;
for(; this.writePos < this.capacity; this.writePos++){
this.elements[this.writePos] = newElements[readPos++];
}
//fill into bottom of array too.
this.writePos = 0;
int endPos = Math.min(length - readPos, capacity - available - readPos);
for(;this.writePos < endPos; this.writePos++){
this.elements[this.writePos] = newElements[readPos++];
}
this.available += readPos;
return readPos;
}
} else {
int endPos = this.capacity - this.available + this.writePos;
for(; this.writePos < endPos; this.writePos++){
this.elements[this.writePos] = newElements[readPos++];
}
this.available += readPos;
return readPos;
}
}
public Object take() {
if(available == 0){
return null;
}
int nextSlot = writePos - available;
if(nextSlot < 0){
nextSlot += capacity;
}
Object nextObj = elements[nextSlot];
available--;
return nextObj;
}
public int take(Object[] into){
return take(into, into.length);
}
public int take(Object[] into, int length){
int intoPos = 0;
if(available <= writePos){
int nextPos= writePos - available;
int endPos = nextPos + Math.min(available, length);
for(;nextPos < endPos; nextPos++){
into[intoPos++] = this.elements[nextPos];
}
this.available -= intoPos;
return intoPos;
} else {
int nextPos = writePos - available + capacity;
int leftInTop = capacity - nextPos;
if(length <= leftInTop){
//copy directly
for(; intoPos < length; intoPos++){
into[intoPos] = this.elements[nextPos++];
}
this.available -= length;
return length;
} else {
//copy top
for(; nextPos < capacity; nextPos++){
into[intoPos++] = this.elements[nextPos];
}
//copy bottom - from 0 to writePos
nextPos = 0;
int leftToCopy = length - intoPos;
int endPos = Math.min(writePos, leftToCopy);
for(;nextPos < endPos; nextPos++){
into[intoPos++] = this.elements[nextPos];
}
this.available -= intoPos;
return intoPos;
}
}
}
}
Ring Buffer Using Flip Marker - Including Batch Operations
Here is an implementation of the ring buffer that uses a read position and flip marker, including the
batch put() and take() operations.
public class RingBufferFlip {
public Object[] elements = null;
public int capacity = 0;
public int writePos = 0;
public int readPos = 0;
public boolean flipped = false;
public RingBufferFlip(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
}
public void reset() {
this.writePos = 0;
this.readPos = 0;
this.flipped = false;
}
public int available() {
if(!flipped){
return writePos - readPos;
}
return capacity - readPos + writePos;
}
public int remainingCapacity() {
if(!flipped){
return capacity - writePos;
}
return readPos - writePos;
}
public boolean put(Object element){
if(!flipped){
if(writePos == capacity){
writePos = 0;
flipped = true;
if(writePos < readPos){
elements[writePos++] = element;
return true;
} else {
return false;
}
} else {
elements[writePos++] = element;
return true;
}
} else {
if(writePos < readPos ){
elements[writePos++] = element;
return true;
} else {
return false;
}
}
}
public int put(Object[] newElements, int length){
int newElementsReadPos = 0;
if(!flipped){
//readPos lower than writePos - free sections are:
//1) from writePos to capacity
//2) from 0 to readPos
if(length <= capacity - writePos){
//new elements fit into top of elements array - copy directly
for(; newElementsReadPos < length; newElementsReadPos++){
this.elements[this.writePos++] = newElements[newElementsReadPos];
}
return newElementsReadPos;
} else {
//new elements must be divided between top and bottom of elements array
//writing to top
for(;this.writePos < capacity; this.writePos++){
this.elements[this.writePos] = newElements[newElementsReadPos++];
}
//writing to bottom
this.writePos = 0;
this.flipped = true;
int endPos = Math.min(this.readPos, length - newElementsReadPos);
for(; this.writePos < endPos; this.writePos++){
this.elements[writePos] = newElements[newElementsReadPos++];
}
return newElementsReadPos;
}
} else {
//readPos higher than writePos - free sections are:
//1) from writePos to readPos
int endPos = Math.min(this.readPos, this.writePos + length);
for(; this.writePos < endPos; this.writePos++){
this.elements[this.writePos] = newElements[newElementsReadPos++];
}
return newElementsReadPos;
}
}
public Object take() {
if(!flipped){
if(readPos < writePos){
return elements[readPos++];
} else {
return null;
}
} else {
if(readPos == capacity){
readPos = 0;
flipped = false;
if(readPos < writePos){
return elements[readPos++];
} else {
return null;
}
} else {
return elements[readPos++];
}
}
}
public int take(Object[] into, int length){
int intoWritePos = 0;
if(!flipped){
//writePos higher than readPos - available section is writePos - readPos
int endPos = Math.min(this.writePos, this.readPos + length);
for(; this.readPos < endPos; this.readPos++){
into[intoWritePos++] = this.elements[this.readPos];
}
return intoWritePos;
} else {
//readPos higher than writePos - available sections are
//top + bottom of elements array
if(length <= capacity - readPos){
//length is lower than the elements available at the top
//of the elements array - copy directly
for(; intoWritePos < length; intoWritePos++){
into[intoWritePos] = this.elements[this.readPos++];
}
return intoWritePos;
} else {
//length is higher than elements available at the top of the elements array
//split copy into a copy from both top and bottom of elements array.
//copy from top
for(; this.readPos < capacity; this.readPos++){
into[intoWritePos++] = this.elements[this.readPos];
}
//copy from bottom
this.readPos = 0;
this.flipped = false;
int endPos = Math.min(this.writePos, length - intoWritePos);
for(; this.readPos < endPos; this.readPos++){
into[intoWritePos++] = this.elements[this.readPos];
}
return intoWritePos;
}
}
}
}
| Tweet | |
Jakob Jenkov | |











